近日，控制领域国际顶级期刊IEEE Transactions on Automatic Control以全文论文（Full Paper）形式在线发表了肉漫屋 研究团队关于不确定Euler-Lagrange系统在聚合优化背景下的两类优化控制算法的研究成果。论文第一作者是我院博士后房肖，通讯作者是我院温广辉教授。

  群体具身智能的核心挑战之一，在于如何为具备真实物理动力学特性的群体系统，实现高效的实时决策与连续控制。Euler-Lagrange系统因能对移动机器人、航天器、自主车辆等各类具身载体的动力学行为进行通用且精准的建模，已成为研究该类问题的核心工具。在此背景下，论文针对不确定Euler-Lagrange系统的聚合优化问题展开研究，分别设计了开环优化控制算法与闭环优化控制算法。从理论特性、适用场景、控制效能等维度，对两种算法进行了系统的对比分析，为后续不确定动力学场景下群体具身系统的优化控制提供了方法支撑与选择依据。

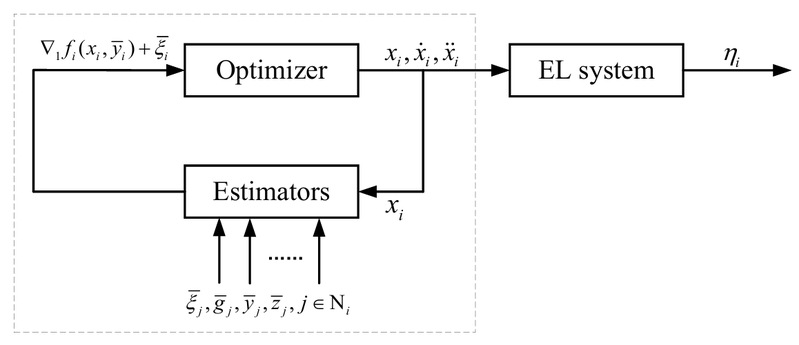
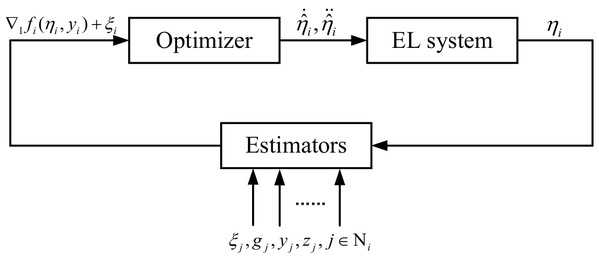
                                                       开环优化控制方法                                                                                 闭环优化控制方法

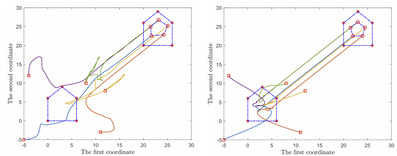
                                                                              (a) 开环方法下航行器运行轨迹             (b) 闭环方法下航行器运行轨迹

  开环与闭环优化控制方法在海上航行器动态最优定位中的应用对比：

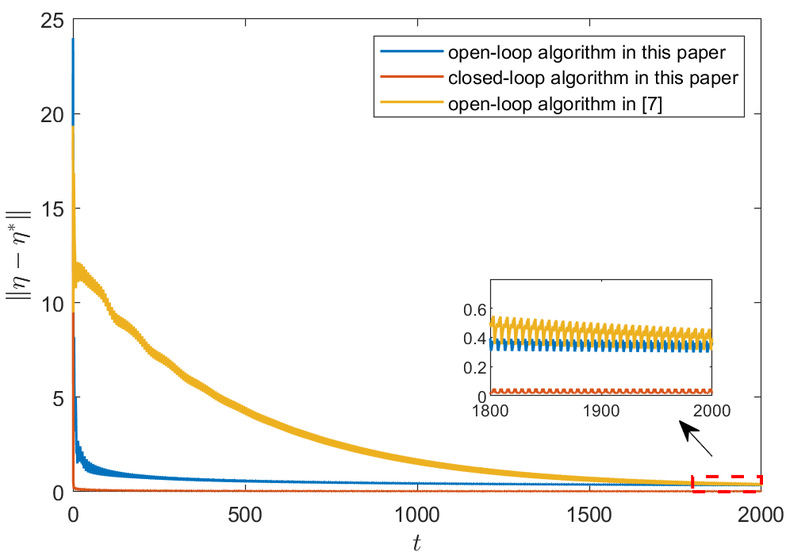
论文所提两种算法相较于现有算法的鲁棒性对比

  开环优化控制方法通过解耦优化与控制模块、引入辅助系统简化设计，参数调节直观，但鲁棒性较弱，更适用于干扰小、工况明确的场景；闭环优化控制方法嵌入实时状态与误差反馈，构建强鲁棒性耦合框架，虽参数要求更高，但动态适应能力突出，适配复杂动态场景（如复杂洋流中海洋航行器、动态环境多机器人系统）。两种方法的创新，既为不确定Euler-Lagrange系统聚合优化提供差异化路径，也为群体具身智能领域工程实践提供实用决策参考，助力相关技术在复杂工况下稳定高效运行。

  论文链接：//ieeexplore.ieee.org/document/11192750